QHELIX

Analyzing how secondary structural elements assemble into a tertiary structure is an important step to understand the folding and functionality of proteins. The alpha-helix is a well-defined common secondary element. The calculation of inter-helical orientation, which can be defined as a tilt angle between different two helices, has been a major geometric determinant to annotate and compare the structural characteristics of proteins. In addition, for proteins undergoing large conformational changes, analyzing the inter-helical tilt angle may provide a detailed description of the structural rearrangements during these events.

QHELIX is an improved computational framework to analyze the orientation of alpha-helix pairs in proteins or any protein complexes.

To obtain helix axes, we used two optional algorithms, which are refered to Chou method (1) and Kahn method (2,3), based on fast, non-iterative linear fitting procedures. Absolute mathematical regularity of the helical parameters is not required for determining helix axes. The present program is capable of straightforwardly assigning the orientation direction as well as calculating the angle between two helices. In addition to the inter-helical angle calculation, the program provides the quantitative measurement on the irregularity of helical shape, resulting in discriminating irregular-shaped helices from helices with an ideal geometry.

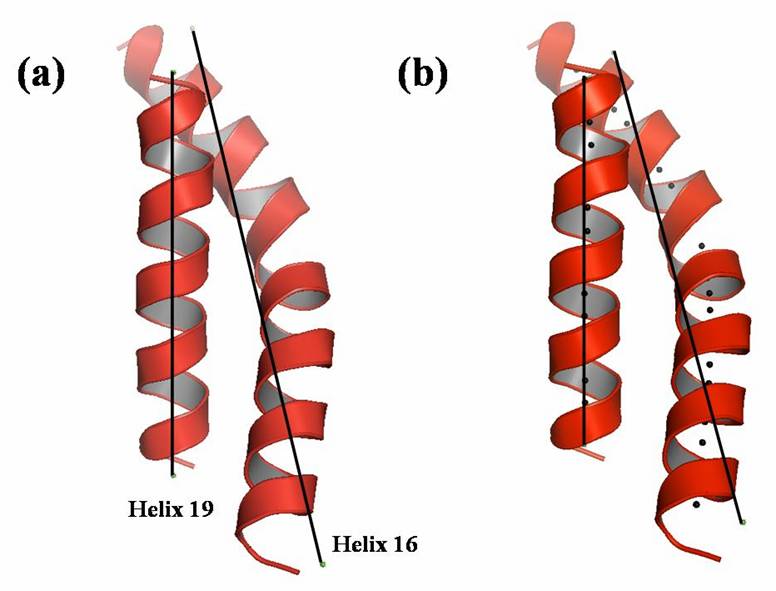
Figure. Graphical presentation of helix axes defined by Chou method and Kahn method in a model system containing an irregularly curved long helix. The axes of the helices 16 (residue range 378-408) and 19 (residue range 462-481) of acetohydroxy acid isomeroreductase (PDB entry: 1YVE) are calculated by (a) Chou method and (b) Kahn method. The axes defined are shown as bold lines. The curvature calculated by Kahn method is depicted as black spheres in (b).

Table. Comparison of inter-helical angle between helix 16 and 19 (theta 16-19), and average displacement distances (d_avg) between an irregularly curved helix (helix 16) and a helix with an ideal geometry (helix 19).